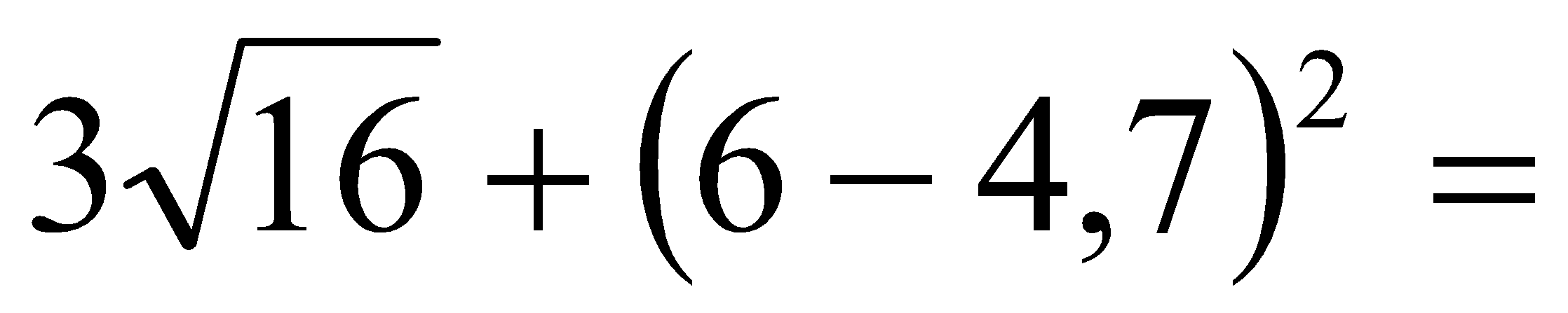5.2.1.a
Dodatek k 5.2.1.:
Učební osnovy předmětu Matematika posíleny o Standardy
STANDARDY
MATEMATIKA
Vypracovala skupina pro přípravu standardů z matematiky ve složení:
Vedoucí: Eduard Fuchs, Přírodovědecká fakulta MU Brno
Koordinátor za VÚP: Eva Zelendová, VÚP v Praze
Členové: Helena Fučíková, ZŠ Praha-Hostivař
Dag Hrubý, Gymnázium Jevíčko
Hana Lišková, VOŠP a SPgŠ Litomyšl
Michaela Pažoutová, ZŠ Praha 4,
Dagmar Ryčlová, ZŠ Jesenice
Jitka Topičová, ZŠ a MŠ Sadov
1. stupeň
1. ČÍSLO A POČETNÍ OPERACE
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Číslo a početní operace |
|
Očekávaný výstup RVP ZV |
M-5-1-01 Žák využívá při pamětném i písemném počítání komutativnost a asociativnost sčítání a násobení |
|
Indikátory |
1.žák zpaměti sčítá a odčítá čísla do sta, násobí a dělí v oboru malé násobilky 2.žák využívá komutativnost sčítání a násobení při řešení úlohy a při provádění zkoušky výpočtu 3.žák využívá asociativnost sčítání a násobení při řešení úloh s užitím závorek 4.žák využívá výhodného sdružování čísel při sčítání několika sčítanců bez závorek |
|
Ilustrační úloha |
|
|
Doplň chybějící čísla:
8 x = 40 
8 + 8 x = 40 
(8 + 4) x 5 = 
|
|
|
Poznámky1 |
M-5-1-01.1
Je-li rámeček vložen vlevo od rovnítka, musí žák pro výpočet zvolit inverzní početní operaci, aby získal výsledek do příslušného rámečku. To je náročnější varianta, než kdyby byl rámeček vpravo od rovnítka. Nutno ponechat oba typy. |
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Číslo a početní operace |
|
Očekávaný výstup RVP ZV |
M-5-1-02 Žák provádí písemné početní operace v oboru přirozených čísel |
|
Indikátory |
1.žák správně sepíše čísla pod sebe (dle číselných řádů) při sčítání, odčítání, násobení a dělení přirozených čísel 2.žák aplikuje při písemném výpočtu znalost přechodu mezi číselnými řády 3.žák využívá znalosti malé násobilky při písemném násobení a dělení nejvýše dvojciferným číslem 4.žák provádí písemné početní operace včetně kontroly výsledku 5.žák dodržuje pravidla pro pořadí operací v oboru přirozených čísel |
|
Ilustrační úloha |
|
|
Vypočítej, do rámečků doplň chybějící číslice:
929 437 328 28 - 154 x 7
          
19 209 : 8 = zb.    
|
|
|
Poznámky |
M-5-1-02.1 M-5-1-02.2 M-5-1-02.3
Tyto úlohy, které vyžadují elementární dovednosti, je nutné zařadit do každého testu. |
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Číslo a početní operace |
|
Očekávaný výstup RVP ZV |
M-5-1-03 Žák zaokrouhluje přirozená čísla, provádí odhady a kontroluje výsledky početních operací v oboru přirozených čísel |
|
Indikátory |
1.žák přečte a zapíše číslo (do milionů) s užitím znalosti číselných řádů desítkové soustavy 2.žák využívá rozvinutého zápisu čísla (do milionů) v desítkové soustavě 3.žák porovnává čísla do milionů 4.žák zaokrouhluje čísla do milionů s použitím znaku pro zaokrouhlování 5.žák užívá polohové vztahy („hned před“, „hned za“) v oboru přirozených čísel 6.žák se orientuje na číselné ose a jejích úsecích 7.žák provádí číselný odhad a kontrolu výsledku |
|
Ilustrační úloha |
|
|
Odhadni a vepiš čísla uvedená v nabídce do rámečků nad číselnou osou. Nabídka čísel:
149 999 852 011 250 100 549 900 308 000

0 100 000 200 000 300 000 400 000 500 000 600 000 700 000 800 000 900 000 1 000 000
|
|
|
Poznámky |
M-5-1-03.6 |
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Číslo a početní operace |
|
Očekávaný výstup RVP ZV |
M-5-1-04 Žák řeší a tvoří úlohy, ve kterých aplikuje osvojené početní operace v celém oboru |
|
Indikátory |
1.žák porozumí textu úlohy (rozlišuje informace důležité pro řešení úlohy) 2.žák přiřadí úloze správné matematické vyjádření s využitím osvojených početních operací 3.žák zformuluje odpověď k získanému výsledku 4.žák přiřadí k zadanému jednoduchému matematickému vyjádření smysluplnou slovní úlohu (situaci ze života) 5.žák tvoří slovní úlohu k matematickému vyjádření |
|
Ilustrační úloha |
|
|
Přiřaď k jednotlivým úlohám odpovídající matematické vyjádření: 36 + 4 = 36 – 4= 36 x 4 = 36: 4 = Úlohy vyřeš.
1.Mamince je 36 let. Její dcera je čtyřikrát mladší. Kolik let je dceři? Matematické vyjádření 
Odpověď: Dceři je _______ roků. 2.Pavel měl ve sbírce 36 modelů letadel. Od dědečka dostal 4 nové modely. Kolik modelů letadel má nyní celkem? Matematické vyjádření 
Odpověď: Pavel má nyní celkem ______ modelů. 3.V počítačové učebně bylo původně 36 počítačů. 4 počítače však již byly zastaralé a poruchové, proto byly z učebny odstraněny. Kolik počítačů v učebně zůstalo?  Matematické vyjádření
Odpověď: V učebně zůstalo ______ počítačů. 4.Ve školní jídelně připravovala kuchařka 4 mísy s jablky. V každé míse bylo 36 jablek. Kolik jablek měla kuchařka celkem? Matematické vyjádření 
Odpověď: Kuchařka měla celkem ______ jablek. |
|
|
Poznámky |
M-5-1-04.1 M-5-1-04.2
Záměrně jsou použita stejná čísla, aby nebylo možné přiřadit úlohu k matematickému vyjádření jen na základě shody číselných údajů.
Indikátory 3 a 5 lze testovat pouze otevřenou úlohou. |
2. ZÁVISLOSTI, VZTAHY A PRÁCE S DATY
|
Vzdělávací obor |
Matematika |
||||||||
|
Ročník |
5. |
||||||||
|
Tematický okruh |
Závislosti, vztahy a práce s daty |
||||||||
|
Očekávaný výstup RVP ZV |
M-5-2-01 Žák vyhledává, sbírá a třídí data |
||||||||
|
Indikátory |
1.žák provádí a zapisuje jednoduchá pozorování (měření teploty, průjezd aut za daný časový limit apod.) 2.žák vybírá a porovnává ze zadání úlohy data podle daného kritéria 3.žák posuzuje reálnost vyhledaných údajů |
||||||||
|
Ilustrační úloha |
|||||||||
|
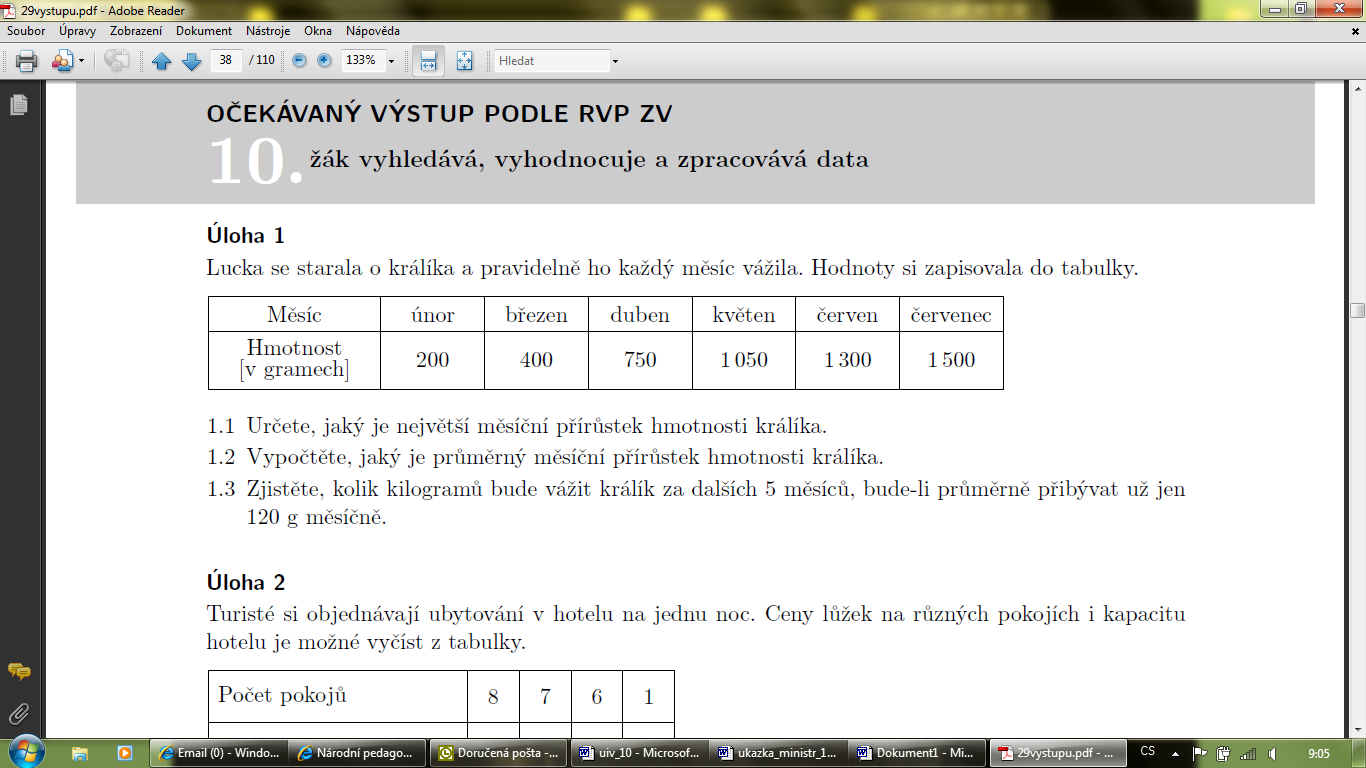
V tabulce je uveden počet diváků, kteří se během uvedených tří dnů přišli podívat do pražských kin na film Kuky se vrací.
1.O kolik bylo návštěvníků v pátek víc než ve středu? __________
2.Kolik návštěvníků celkem vidělo film v uvedených dnech? _________
3.Je z údajů možné určit, kolik návštěvníků vidělo tento film v sobotu? ANO – NE (zakroužkuj pravdivou odpověď)
|
|||||||||
|
Poznámky |
M-5-2-01.2
Indikátor 1 nelze testovat elektronicky. |
||||||||
|
Vzdělávací obor |
Matematika |
||||||||
|
Ročník |
5. |
||||||||
|
Tematický okruh |
Závislosti, vztahy a práce s daty |
||||||||
|
Očekávaný výstup RVP ZV |
M-5-2-02 Žák čte a sestavuje jednoduché tabulky a diagramy |
||||||||
|
Indikátory |
1.žák doplní údaje do připravené tabulky nebo diagramu 2.žák vytvoří na základě jednoduchého textu tabulku, sloupcový diagram 3.žák vyhledá v tabulce nebo diagramu požadovaná data a porozumí vztahům mezi nimi (nejmenší, největší hodnota apod.) 4.žák používá údaje z různých typů diagramů (sloupcový a kruhový diagram bez použití %) 5.žák používá jednoduchých převodů jednotek času při práci s daty v jízdních řádech |
||||||||
|
Ilustrační úloha – minimální obtížnost |
|||||||||
|
Na informační tabuli o příjezdech vlaků jsou tyto údaje:
Vyber z nabídky, v kolik hodin přijede zpožděný vlak
a) 19:35 b) 13:45 c) 13:35 d) 13:05
|
|||||||||
|
Poznámky |
M-5-2-02.3
Indikátor 2 nelze testovat elektronicky. |
||||||||
3. GEOMETRIE V ROVINĚ A V PROSTORU
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Geometrie v rovině a v prostoru |
|
Očekávaný výstup RVP ZV |
M-5-3-01 Žák narýsuje a znázorní základní rovinné útvary (čtverec, obdélník, trojúhelník a kružnice); užívá jednoduché konstrukce |
|
Indikátory |
1.žák rozezná základní rovinné útvary (čtverec, obdélník, trojúhelník a kružnice) 2.žák využívá k popisu rovinného útvaru počty vrcholů a stran, rovnoběžnost a kolmost stran 3.žák charakterizuje základní rovinné útvary a k zadanému popisu přiřadí název základního rovinného útvaru 4.žák využívá základní pojmy a značky užívané v rovinné geometrii (čáry: křivá, lomená, přímá; bod, úsečka, polopřímka, přímka, průsečík, rovnoběžky, kolmice) 5.žák využije znalosti základních rovinných útvarů k popisu a modelování jednoduchých těles (krychle, kvádr, válec) 6.žák narýsuje kružnici s daným poloměrem 7.žák narýsuje trojúhelník nebo trojúhelník se třemi zadanými délkami stran 8.žák narýsuje čtverec a obdélník s užitím konstrukce rovnoběžek a kolmic 9.žák dodržuje zásady rýsování |
|
Ilustrační úloha |
|
|
K popisu rovinných útvarů přiřaď správný název a obrázek (A, B, C,D).
1. Útvar má 4 strany. Všechny sousední strany jsou kolmé. Všechny strany mají stejnou délku. _______________ 2. Útvar má 4 vrcholy. Protilehlé strany jsou vždy rovnoběžné. Sousední strany mají různou délku. ____________ 3. Útvar má 3 strany a 3 vrcholy. ___________________
4. Útvar nemá žádnou stranu ani vrchol. _____________
Nabídka názvů: kružnice obdélník trojúhelník čtverec    
A B C D
|
|
|
Poznámky |
M-5-3-01.1 M-5-3-01.3
Indikátory 6 – 9 nelze testovat elektronicky. |
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Geometrie v rovině a v prostoru |
|
Očekávaný výstup RVP ZV |
M-5-3-02 Žák sčítá a odčítá graficky úsečky; určí délku lomené čáry, obvod mnohoúhelníku sečtením délek jeho stran |
|
Indikátory |
1.žák rozlišuje obvod a obsah rovinného útvaru 2.žák s pomocí čtvercové sítě nebo měřením určí obvod rovinného útvaru (trojúhelníku, čtyřúhelníku, mnohoúhelníku) 3.žák porovnává obvody rovinných útvarů 4.žák graficky sčítá, odčítá a porovnává úsečky 5.žák určí délku lomené čáry graficky i měřením 6.žák převádí jednotky délky (mm, cm, dm, m, km) |
|
Ilustrační úloha |
|
|
Na obrázku jsou tři rovinné útvary K, L, N.
Rozhodněte o každém z následujících tvrzení, zda platí (ANO), nebo neplatí (NE).   1. Obdélníky K a N mají stejný obvod. ANO NE   2. Obdélník K má větší obvod než útvar L. ANO NE
|
|
|
Poznámky |
M-5-3-02.1 M-5-3-02.2 M-5-3-02.3
Nutno vložit jako podklad celého obrázku čtvercovou síť.
Indikátory 4 a 5, částečně 2 nelze testovat elektronicky. |
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-5-3-03 Žák sestrojí rovnoběžky a kolmice |
|
Indikátory |
1.žák vyhledá dvojice kolmic a rovnoběžek v rovině 2.žák načrtne kolmici a rovnoběžku ve čtvercové síti 3.žák narýsuje k zadané přímce rovnoběžku a kolmici vedoucí daným bodem pomocí trojúhelníku s ryskou |
|
Ilustrační úloha |
|
|
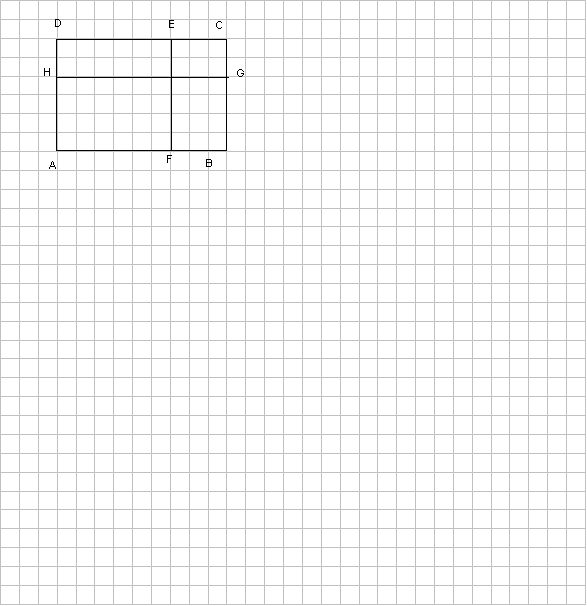
Rozhodněte o každém z následujících tvrzení o úsečkách na obrázku, zda platí (ANO), nebo neplatí (NE).
Úsečky AD a HG jsou kolmé ANO NE 
Úsečky EH a EG jsou rovnoběžné ANO NE
Úsečky EF a AD jsou rovnoběžné ANO NE     Úsečky AH a FA jsou kolmé ANO NE
|
|
|
Poznámky |
M-5-3-03.1
Nutno vložit jako podklad celého obrázku čtvercovou síť.
Indikátor 2 nelze testovat elektronicky. |
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Geometrie v rovině a v prostoru |
|
Očekávaný výstup RVP ZV |
M-5-3-04 Žák určí obsah obrazce pomocí čtvercové sítě a užívá základní jednotky obsahu |
|
Indikátory |
1.žák určí pomocí čtvercové sítě obsah rovinného útvaru, který lze složit ze čtverců, obdélníků a trojúhelníků 2.žák porovnává pomocí čtvercové sítě obsahy rovinných útvarů 3.žák používá základní jednotky obsahu (cm2, m2, km2) bez vzájemného převádění |
|
Ilustrační úloha |
|
|
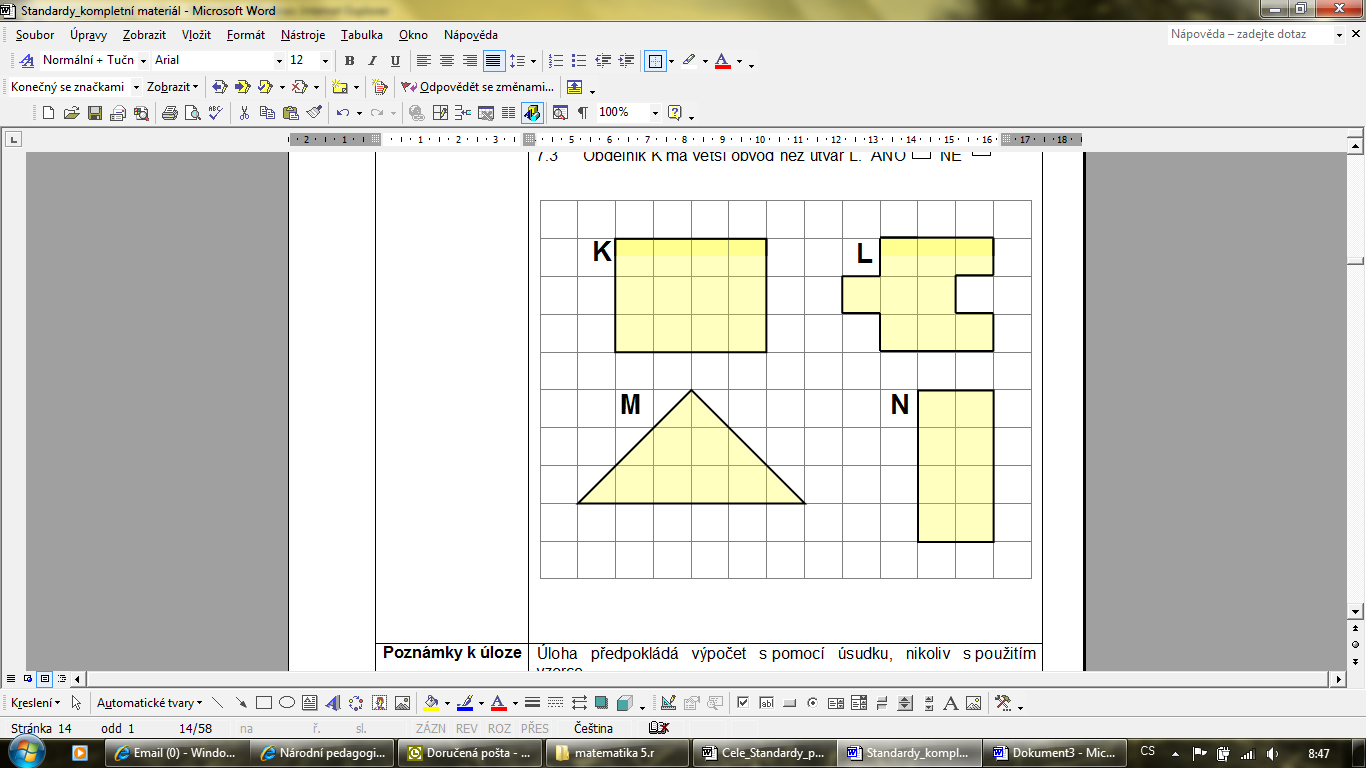
Na obrázku jsou čtyři rovinné útvary K, L,M, N.
Rozhodněte o každém z následujících tvrzení, zda je pravdivé (ANO), nebo nepravdivé (NE).   1. Obdélníky K a N mají stejný obsah. ANO NE   2. Útvary L a M mají stejný obsah. ANO NE   3. Obdélník K má větší obsah než útvar L. ANO NE
|
|
|
Poznámky |
M-5-3-04.1 M-5-3-04.2 |
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Geometrie v rovině a v prostoru |
|
Očekávaný výstup RVP ZV |
M-5-3-05 Žák rozpozná a znázorní ve čtvercové síti jednoduché osově souměrné útvary a určí osu souměrnosti útvaru překládáním papíru |
|
Indikátory |
1.žák pozná osově souměrné útvary (i v reálném životě) 2.žák určí překládáním papíru osu souměrnosti útvaru 3.žák vytvoří ve čtvercové síti osově souměrný útvar podle osy v lince mřížky |
|
Ilustrační úloha |
|
|
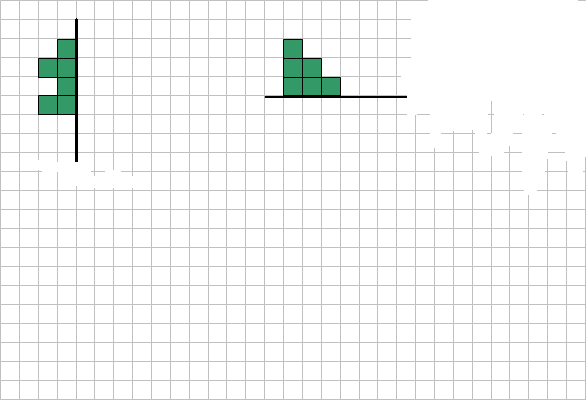
Doplň obrázky tak, aby vznikly osově souměrné útvary podle vyznačené osy souměrnosti.
|
|
|
Poznámky |
M-5-3-05.3
Indikátor 2 nelze testovat elektronicky. |
4. NESTANDARDNÍ APLIKAČNÍ ÚLOHY A PROBLÉMY
|
Vzdělávací obor |
Matematika |
|
Ročník |
5. |
|
Tematický okruh |
Nestandardní aplikační úlohy a problémy |
|
Očekávaný výstup RVP ZV |
M-5-4-01 |
|
Indikátory |
1.žák vyhledá v textu úlohy potřebné údaje a vztahy 2.žák volí vhodné postupy pro řešení úlohy 3.žák vyhodnotí výsledek úlohy |
|
Ilustrační úloha |
|
|
Maminka chce upéct perník. Troubu musí předehřát 15 minut a potom 40 minut bude perník péci. Perník má být upečený v jedenáct hodin. Kdy nejpozději musí maminka troubu zapnout?
a) 10:05 b) 10:15 c) 10:25 d) 10:55
|
|
|
Poznámky |
M-5-4-01.1 M-5-4-01.2 M-5-4-01.3 |
2. stupeň
1. ČÍSLO A PROMĚNNÁ
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Číslo a proměnná |
|
Očekávaný výstup RVP ZV |
M-9-1-01 Žák provádí početní operace v oboru celých a racionálních čísel; užívá ve výpočtech druhou mocninu a odmocninu |
|
Indikátory |
1.žák provádí základní početní operace se zlomky a desetinnými čísly 2.žák dodržuje pravidla pro pořadí početních operací v oboru celých a racionálních čísel, využívá vlastností operací sčítání a násobení (komutativnost, asociativnost, distributivnost) při úpravě výrazů 3.žák vyznačí na číselné ose racionální číslo a číslo k němu opačné 4.žák užívá znalosti druhých mocnin celých čísel od 1 do 20 (i ke stanovení odpovídajících druhých odmocnin) 5.žák určí rozvinutý zápis přirozeného čísla v desítkové soustavě 6.žák provádí základní úpravy zlomků (rozšiřuje a krátí zlomek, zjednoduší složený zlomek, vyjádří zlomek v základním tvaru, určí převrácené číslo, počítá se smíšenými čísly) 7.žák určí absolutní hodnotu celého čísla a využívá její geometrickou interpretaci |
|
Ilustrační úloha |
|
|
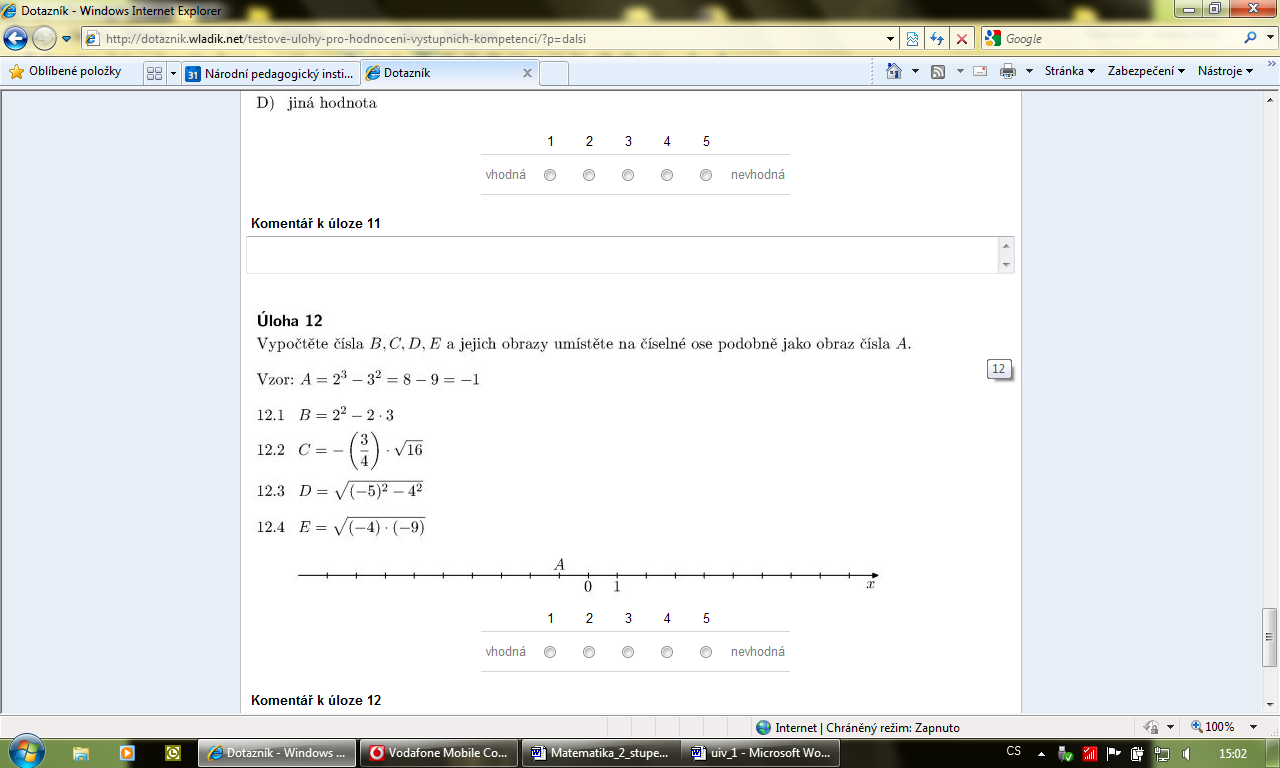
Vypočtěte hodnoty B, C, D, E a jejich obrazy umístěte na číselné ose podobně jako obraz čísla A.
Vzor: A = 10 . 12 – 112 = 120 – 121 = – 1
|
|
|
Poznámky |
M-9-1-01.3 M-9-1-01.4 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Číslo a proměnná |
|
Očekávaný výstup RVP ZV |
M-9-1-02 Žák zaokrouhluje a provádí odhady s danou přesností, účelně využívá kalkulátor |
|
Indikátory |
1.žák zaokrouhluje čísla s danou přesností 2.žák využívá pro kontrolu výsledku odhad 3.žák účelně a efektivně využívá kalkulátor |
|
Ilustrační úloha |
|
|
Vypočtěte hodnoty A, B a výsledek zaokrouhlete na jedno desetinné místo:
A = 0,6 . 5 – 1,22 =
B =
|
|
|
Poznámky |
M-9-1-02.1 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Číslo a proměnná |
|
Očekávaný výstup RVP ZV |
M-9-1-03 Žák modeluje a řeší situace s využitím dělitelnosti v oboru přirozených čísel |
|
Indikátory |
1.žák rozlišuje pojmy prvočíslo a číslo složené; společný dělitel a společný násobek (určí je pro skupinu dvou nebo tří přirozených čísel) 2.žák najde nejmenší společný násobek a největšího společného dělitele dvou přirozených čísel 3.žák využívá kritéria dělitelnosti (2, 3, 4, 5, 9, 10, 25, 50, 100) 4.žák řeší slovní úlohu s využitím dělitelnosti 5.žák vytvoří slovní úlohu na využití dělitelnosti |
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-1-03.2
Indikátor 5 lze testovat pouze otevřenou úlohou. |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Číslo a proměnná |
|
Očekávaný výstup RVP ZV |
M-9-1-04 Žák užívá různé způsoby kvantitativního vyjádření vztahu celek – část (přirozeným číslem, poměrem, zlomkem, desetinným číslem, procentem) |
|
Indikátory |
1.žák užívá různé způsoby kvantitativního vyjádření vztahu celek – část: přirozeným číslem, poměrem, zlomkem, desetinným číslem, procentem 2.žák navzájem převádí různá vyjádření vztahu celek – část |
|
Ilustrační úloha |
|
|
Abychom dané číslo zvětšili o 5 % musíme je vynásobit číslem
|
|
|
Poznámky |
M-9-1-04.1 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Číslo a proměnná |
|
Očekávaný výstup RVP ZV |
M-9-1-05 Žák řeší modelováním a výpočtem situace vyjádřené poměrem; pracuje s měřítky map a plánů |
|
Indikátory |
1.žák využívá daný poměr (včetně postupného poměru) v reálných situacích 2.žák stanoví poměr ze zadaných údajů 3.žák využívá měřítko mapy, plánu k výpočtu 4.žák umí odvodit měřítko mapy, plánu ze zadaných údajů 5.žák používá při řešení úloh úměru a trojčlenku 6.žák řeší modelováním situace vyjádřené poměrem
|
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-1-05.1 M-9-1-05.4
Indikátor 6 nelze testovat elektronicky. |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Číslo a proměnná |
|
Očekávaný výstup RVP ZV |
M-9-1-06 Žák řeší aplikační úlohy na procenta (i pro případ, že procentová část je větší než celek) |
|
Indikátory |
1.žák vyhledá v textu údaje a vztahy potřebné k výpočtu 2.žák určí počet procent, je-li dána procentová část a základ 3.žák určí procentovou část, je-li dán procentový počet a základ 4.žák určí základ, je-li dán procentový počet a procentová část 5.žák používá procentového počtu při řešení úloh z jednoduchého úrokování 6.žák ověří správnost výsledku aplikační úlohy na procenta |
|
Ilustrační úloha |
|
|
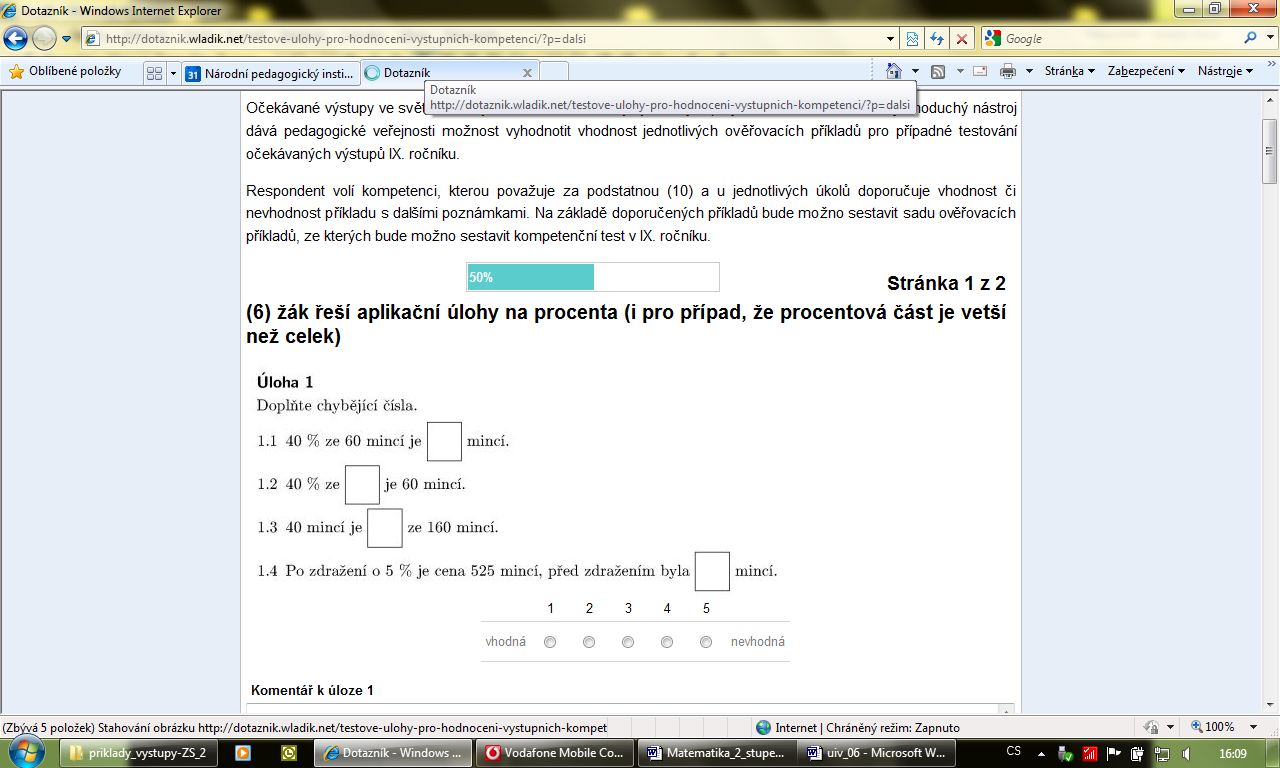
Doplňte chybějící hodnoty.
|
|
|
Poznámky |
M-9-1-06.1 M-9-1-06.2 M-9-1-06.3 M-9-1-06.4 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Číslo a proměnná |
|
Očekávaný výstup RVP ZV |
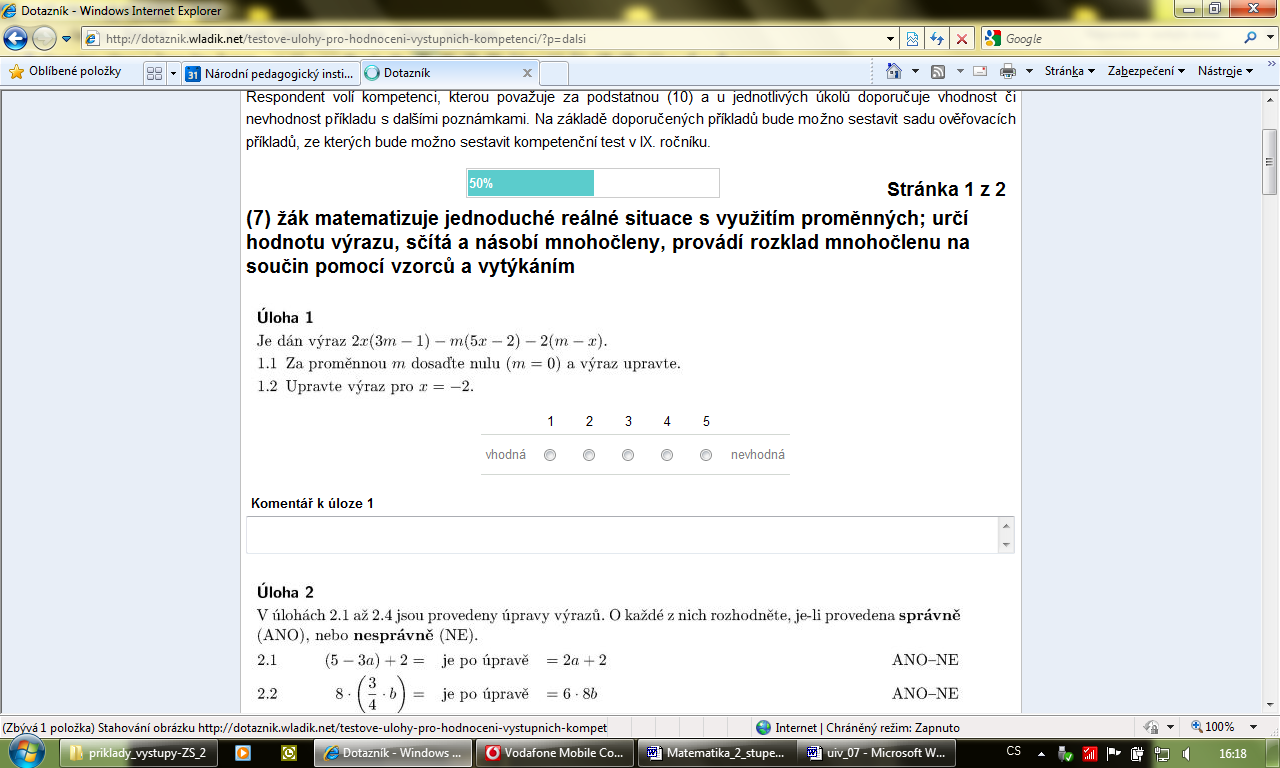
M-9-1-07 Žák matematizuje jednoduché reálné situace s využitím proměnných; určí hodnotu výrazu, sčítá a násobí mnohočleny, provádí rozklad mnohočlenu na součin pomocí vzorců a vytýkáním |
|
Indikátory |
1.žák řeší zadané slovní úlohy pomocí proměnných 2.žák tvoří smysluplné slovní úlohy, které lze řešit užitím proměnných 3.žák využívá při úpravě výrazů sčítání, odčítání a násobení mnohočlenů (výsledný mnohočlen je nejvýše druhého stupně) 4.žák vypočte hodnotu výrazu pro dané hodnoty proměnných 5.žák využívá při úpravě výrazů vytýkání a vzorců (a + b)2, (a – b)2, a2 – b2 6.žák sestaví číselný výraz podle slovního zadání |
|
Ilustrační úloha |
|
|
Upravte původní výraz pro x = – 2.
|
|
|
Poznámky |
M-9-1-07.3 M-9-1-07.4
Indikátor 2 lze testovat pouze otevřenou úlohou. |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Číslo a proměnná |
|
Očekávaný výstup RVP ZV |
M-9-1-08 Žák formuluje a řeší reálnou situaci pomocí rovnic a jejich soustav |
|
Indikátory |
1.žák sestaví rovnici nebo soustavu dvou rovnic o dvou neznámých ze zadaných údajů 2.žák vyřeší rovnici nebo soustavu dvou rovnic o dvou neznámých pomocí ekvivalentních úprav 3.žák provádí zkoušku rovnice nebo soustavy dvou rovnic o dvou neznámých 4.žák ověří správnost řešení slovní úlohy 5.žák přiřadí k rovnici odpovídající slovní úlohu 6.žák rozhodne, zda rovnice nebo soustava rovnic má řešení a ověří, zda řešení patří do zadaného číselného oboru |
|
Ilustrační úloha |
|
|
Šest rohlíku stojí stejně jako pět housek. Rohlík je o padesát haléřů levnější než houska. Kolik korun postačí na nákup deseti rohlíku a pěti housek? A) stačí 30 korun B) 30 korun je málo, ale 35 korun postačí C) 35 korun je málo, ale 40 korun postačí D) nestačí ani 40 korun |
|
|
Poznámky |
M-9-1-08.2 M-9-1-08.3 M-9-1-08.4 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Číslo a proměnná |
|
Očekávaný výstup RVP ZV |
M-9-1-09 Žák analyzuje a řeší jednoduché problémy, modeluje konkrétní situace, v nichž využívá matematický aparát v oboru celých a racionálních čísel |
|
Indikátory |
1.žák vytvoří matematický model konkrétní situace v oboru celých a racionálních čísel 2.žák využívá při řešení konkrétních situací matematický aparát v oboru celých a racionálních čísel 3.žák vyhodnotí výsledek řešení úlohy |
|
Ilustrační úloha |
|
|
Parta kopáčů vyhloubí za osmihodinovou směnu příkop dlouhý 32 metrů.
Jak dlouhý příkop vyhloubí parta za pětidenní pracovní týden? Jak dlouhý příkop parta vyhloubí za jednu hodinu? Za kolik hodin vyhloubí parta 150 metrů příkopu?
|
|
|
Poznámky |
M-9-1-09.1 M-9-1-09.2 M-9-1-09.3
Indikátor 1 lze testovat pouze otevřenou úlohou. |
2. ZÁVISLOSTI, VZTAHY A PRÁCE S DATY
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Závislosti, vztahy a práce s daty |
|
Očekávaný výstup RVP ZV |
M-9-2-01 Žák vyhledává, vyhodnocuje a zpracovává data |
|
Indikátory |
1.žák vyhledá potřebné údaje v tabulce, diagramu a grafu 2.žák vyhledá a vyjádří vztahy mezi uvedenými údaji v tabulce, diagramu a grafu (četnost, aritmetický průměr, nejmenší a největší hodnota) 3.žák zpracuje, porovná, vyhodnotí, uspořádá, doplní uvedené údaje podle zadání úlohy 4.žák pracuje s intervaly a časovou osou 5.žák převádí údaje z textu do tabulky, diagramu a grafu a naopak 6.žák převádí údaje mezi tabulkou, diagramem a grafem 7.žák samostatně vyhledává data v literatuře, denním tisku a na internetu a kriticky hodnotí jejich reálnost |
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-2-01.1 M-9-2-01.2 |
|
Vzdělávací obor |
Matematika a její aplikace |
||||||||
|
Ročník |
9. |
||||||||
|
Tematický okruh |
Závislosti, vztahy a práce s daty |
||||||||
|
Očekávaný výstup RVP ZV |
M-9-2-02 Žák porovnává soubory dat |
||||||||
|
Indikátory |
1.žák porovná kvantitativní vztahy mezi soubory dat zadaných tabulkami, grafy a diagramy 2.žák interpretuje výsledky získané porovnáváním souborů dat |
||||||||
|
Ilustrační úloha |
|||||||||
|
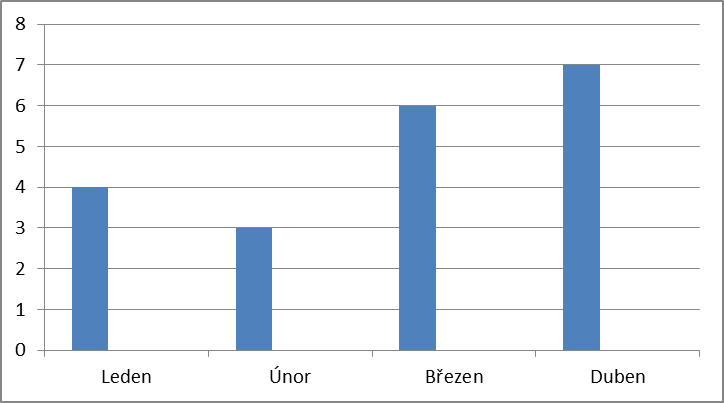
V tabulce je uveden počet domácích úloh z matematiky ve čtyřech po sobě jdoucích měsících v 9. A, diagram udává počet úloh, které ve stejných měsících dostali žáci 9. B.
9. A
9. B
a) Která třída dostala v uvedených měsících více úloh? b) Jaký byl největší počet úloh za měsíc v jednotlivých třídách? c) Jaký byl průměrný počet úloh za měsíc ve třídě A a ve třídě B?
|
|||||||||
|
Poznámky |
M-9-2-02.1 M-9-2-02.2 |
||||||||
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Závislosti, vztahy a práce s daty |
|
Očekávaný výstup RVP ZV |
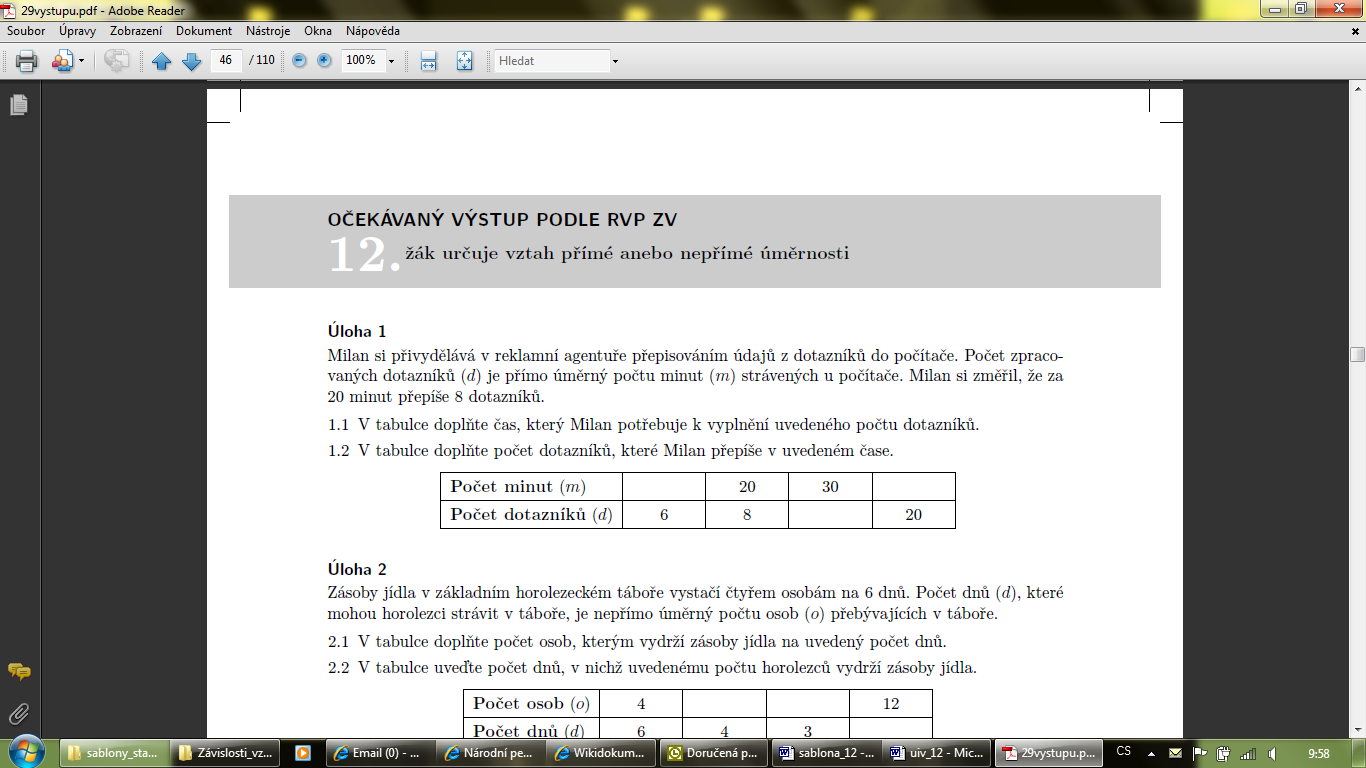
M-9-2-03 Žák určuje vztah přímé anebo nepřímé úměrnosti |
|
Indikátory |
1.žák vytvoří tabulku, graf a rovnici pro přímou a nepřímou úměrnost na základě textu úlohy 2.žák určí přímou a nepřímou úměrnost z textu úlohy, z tabulky, z grafu a z rovnice 3.žák využívá při řešení úloh přímou a nepřímou úměrnost |
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-2-03.2 M-9-2-03.3 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Závislosti, vztahy a práce s daty |
|
Očekávaný výstup RVP ZV |
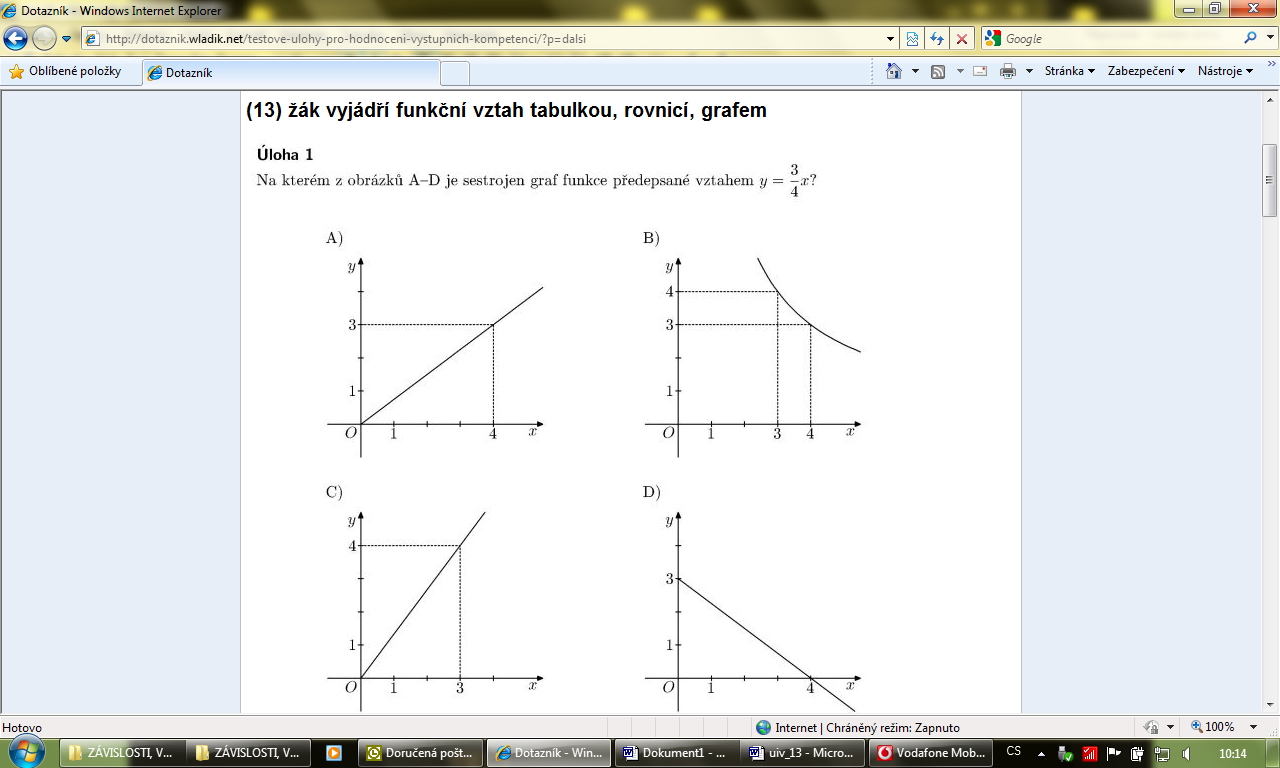
M-9-2-04 Žák vyjádří funkční vztah tabulkou, rovnicí, grafem
|
|
Indikátory |
1.žák pozná funkční závislost z textu úlohy, z tabulky, z grafu a z rovnice 2.žák vytvoří graf pro funkční závislost danou tabulkou či rovnicí 3.žák přiřadí funkční vztah vyjádřený tabulkou k příslušnému grafu a naopak 4.žák přiřadí lineární funkci vyjádřenou rovnicí k příslušnému grafu nebo tabulce a naopak 5.žák vyčte z grafu význačné hodnoty na základě porozumění vzájemným vztahům mezi proměnnými |
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-2-04.3 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Závislosti, vztahy a práce s daty |
|
Očekávaný výstup RVP ZV |
M-9-2-05 Žák matematizuje jednoduché reálné situace s využitím funkčních vztahů |
|
Indikátory |
1.žák odhalí funkční vztahy v textu úlohy 2.žák řeší úlohu s využitím funkčních vztahů 3.žák vyjádří výsledek řešení úlohy v kontextu reálné situace
|
|
Ilustrační úloha |
|
|
Za 1 hodinu nastoupí na vlek celkem 240 lidí. Cesta vlekem nahoru spolu s návratem
|
|
|
Poznámky
|
M-9-2-05.2 M-9-2-05.3 |
3. GEOMETRIE V ROVINĚ A V PROSTORU
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-9-3-01 Žák zdůvodňuje a využívá polohové a metrické vlastnosti základních rovinných útvarů při řešení úloh a jednoduchých praktických problémů; využívá potřebnou matematickou symboliku |
|
Indikátory |
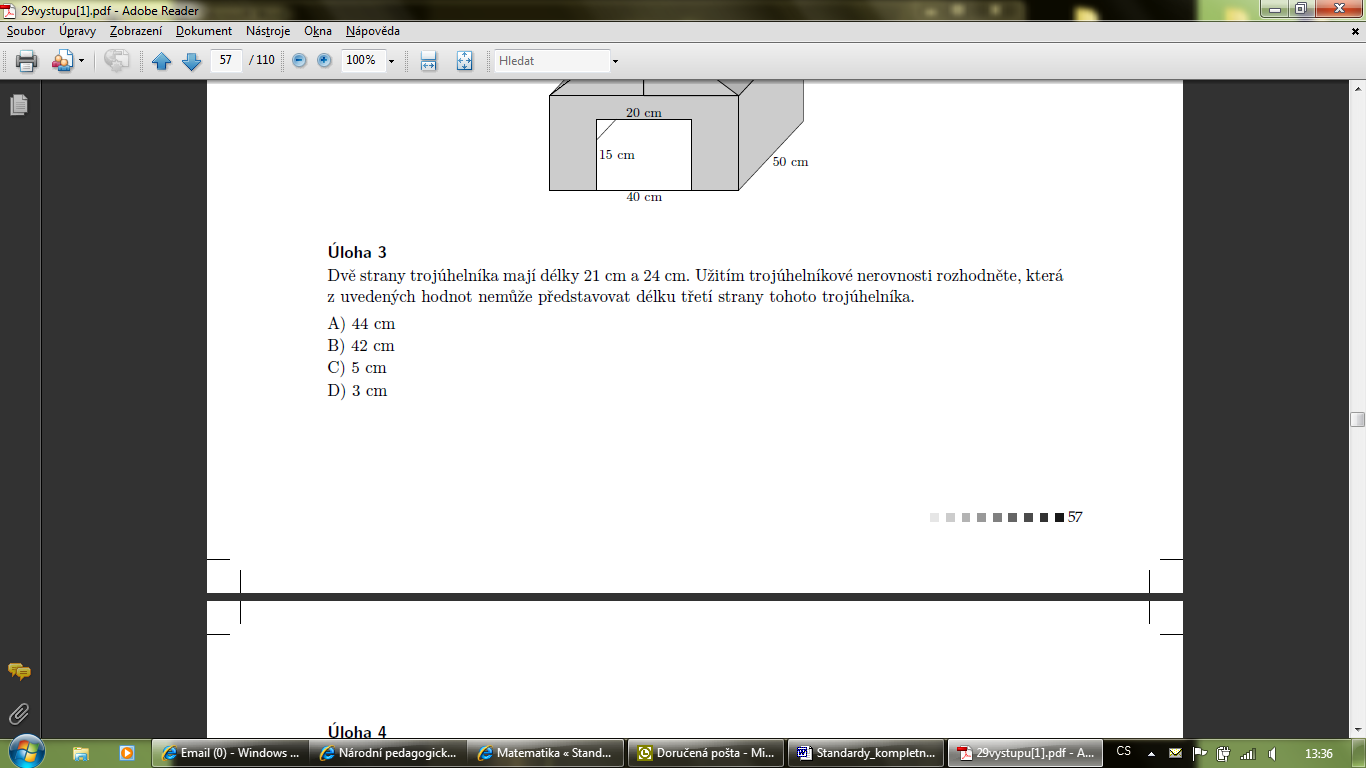
1.žák využívá při analýze praktické úlohy náčrtky, schémata, modely 2.žák využívá polohové a metrické vlastnosti (Pythagorova věta, trojúhelníková nerovnost, vzájemná poloha bodů a přímek v rovině, vzdálenost bodu od přímky) k řešení geometrických úloh 3.žák řeší geometrické úlohy početně 4.žák využívá matematickou symboliku |
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-3-01.2 M-9-3-01.3
Indikátor 1 nelze testovat elektronicky. |
|
Vzdělávací obor |
Matematika a její aplikace |
||||||||||||||||||||||||
|
Ročník |
9. |
||||||||||||||||||||||||
|
Tematický okruh |
Geometrie v rovině a prostoru |
||||||||||||||||||||||||
|
Očekávaný výstup RVP ZV |
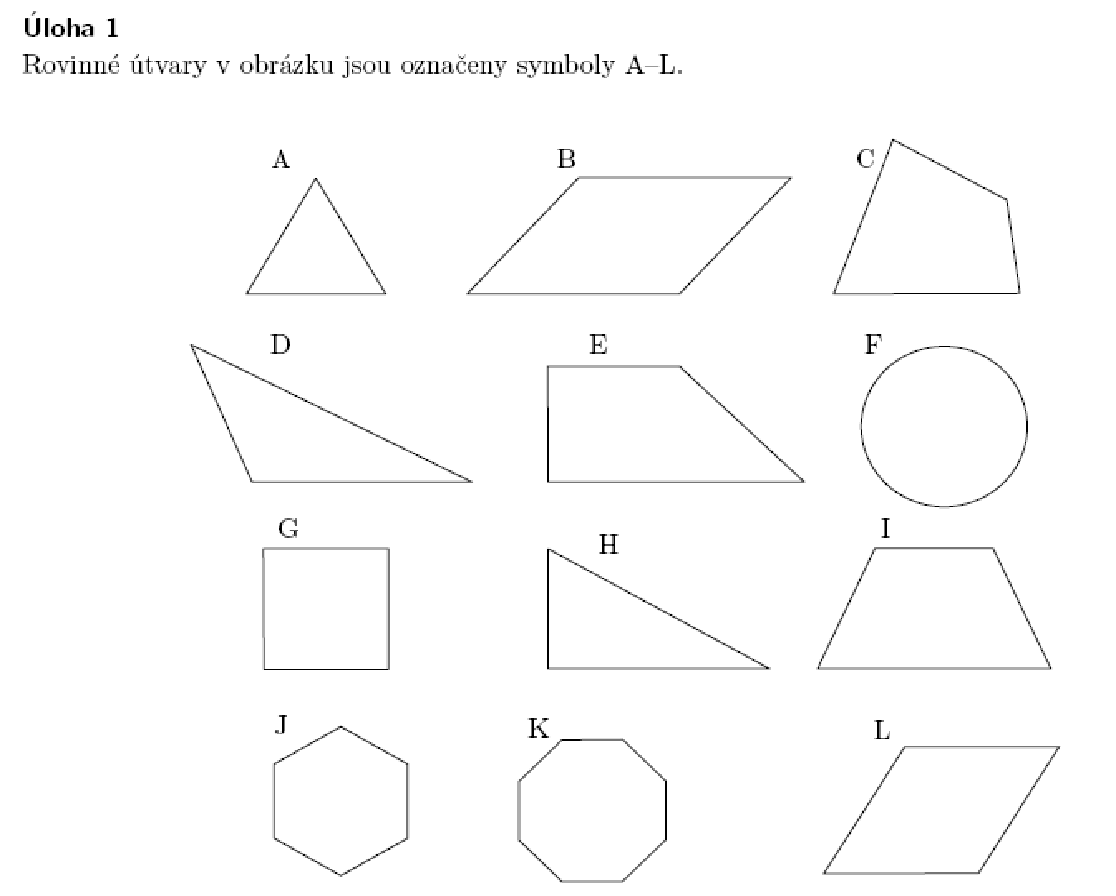
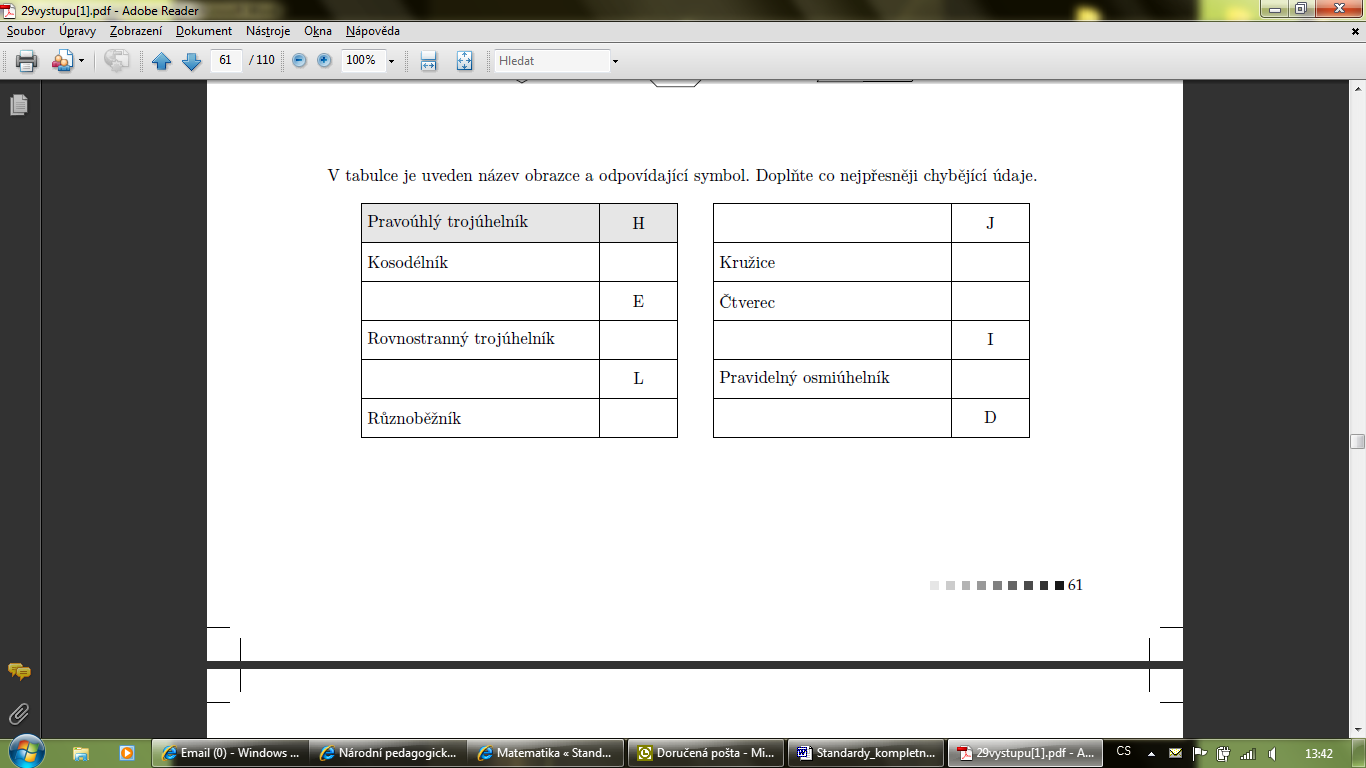
M-9-3-02 Žák charakterizuje a třídí základní rovinné útvary
|
||||||||||||||||||||||||
|
Indikátory |
1.žák pozná základní rovinné útvary: přímka, polopřímka, úsečka, úhel, trojúhelník, čtyřúhelník, pravidelné mnohoúhelníky, kružnice, kruh 2.žák rozliší typy úhlů (ostrý, tupý, pravý, přímý), dvojice úhlů (souhlasné, střídavé, vedlejší, vrcholové), typy trojúhelníků a čtyřúhelníků 3.žák využívá vlastností základních rovinných útvarů (vlastností úhlopříček, velikost úhlů, souměrnost) |
||||||||||||||||||||||||
|
Ilustrační úloha |
|||||||||||||||||||||||||

|
|||||||||||||||||||||||||
|
Poznámky |
M-9-3-02.1 M-9-3-02.2 |
||||||||||||||||||||||||
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-9-3-03 Žák určuje velikost úhlu měřením a výpočtem |
|
Indikátory |
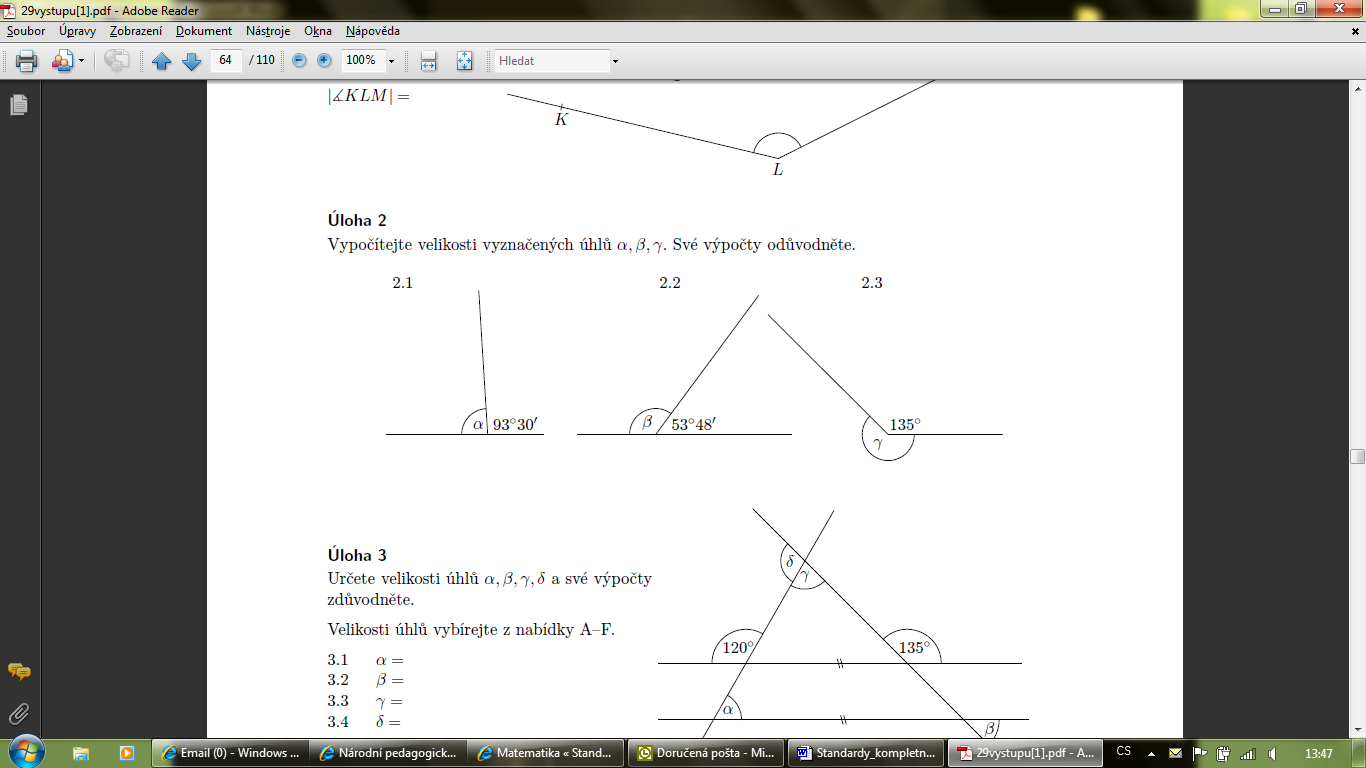
1.žák sčítá a odčítá úhly, určí násobek úhlu (s využitím převodu stupňů a minut)
2.žák využívá při výpočtech vlastností dvojic úhlů (střídavých, souhlasných, vedlejších, vrcholových) a součtu úhlů v trojúhelníku 3.žák určuje velikost úhlu pomocí úhloměru
|
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-3-03.1 M-9-3-03.2 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-9-3-04 Žák odhaduje a vypočítá obsah a obvod základních rovinných útvarů |
|
Indikátory |
1.žák odhaduje obsah i obvod útvarů pomocí čtvercové sítě 2.žák určí výpočtem obsah (v jednodušších případech) trojúhelníku, čtverce, obdélníku, rovnoběžníku, lichoběžníku, kruhu 3.žák určí výpočtem obvod trojúhelníku, čtverce, obdélníku, rovnoběžníku, lichoběžníku, kruhu 4.žák používá a převádí jednotky délky 5.žák používá a převádí jednotky obsahu |
|
Ilustrační úloha |
|
|
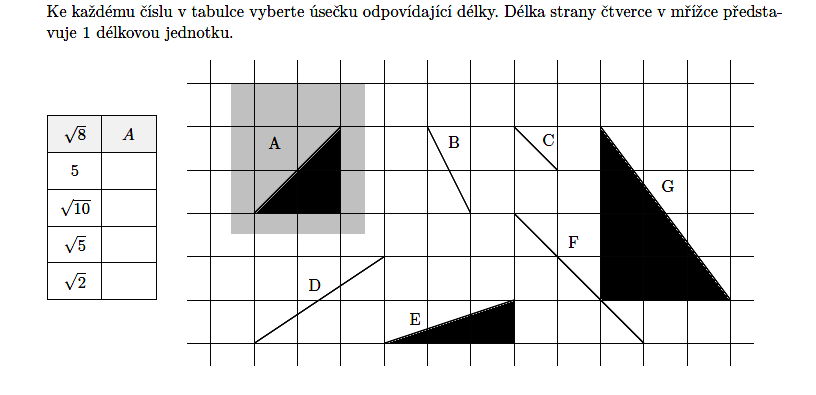
Délka strany čtverce v mřížce je jeden centimetr. Určete obvod a obsah trojúhelníku G.
|
|
|
Poznámky |
M-9-3-04.2 M-9-3-04.3 M-9-3-04.4 M-9-3-04.5 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-9-3-05 Žák využívá pojem množina všech bodů dané vlastnosti k charakteristice útvaru a k řešení polohových a nepolohových konstrukčních úloh |
|
Indikátory |
1.žák pojmenuje základní množiny všech bodů dané vlastnosti (osa úhlu, osa rovinného pásu, osa úsečky, kružnice, Thaletova kružnice) 2.žák využívá množiny všech bodů dané vlastnosti při řešení úloh |
|
Ilustrační úloha |
|
|
Co je množinou všech bodů v rovině, které mají od dvou různých bodů A, B stejnou vzdálenost?
|
|
|
Poznámky |
M-9-3-05.1 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-9-3-06 Žák načrtne a sestrojí rovinné útvary
|
|
Indikátory |
1.žák převede slovní zadání do grafické podoby (náčrtku) 2.žák popíše jednotlivé kroky konstrukce a rovinný útvar sestrojí 3.žák určí počet řešení konstrukční úlohy 4.žák ověří, zda výsledný útvar odpovídá zadání |
|
Ilustrační úloha |
|
|
Sestrojte rovnostranný trojúhelník ABC o délce strany 5 cm. Sestrojte a vybarvěte rovinný útvar, jehož každý bod X má od každého z vrcholu trojúhelníka ABC vzdálenost menší nebo rovnu 4 cm. Popište jednotlivé kroky konstrukce.
|
|
|
Poznámky |
M-9-3-06.1 M-9-3-06.2
Indikátory1 – 4 nelze testovat elektronicky. |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-9-3-07 Žák užívá k argumentaci a při výpočtech věty o shodnosti a podobnosti trojúhelníků |
|
Indikátory |
1.žák využívá při výpočtech věty o shodnosti trojúhelníků 2.žák využívá při výpočtech věty o podobnosti trojúhelníků 3.žák určí poměr podobnosti z rozměrů útvarů a naopak |
|
Ilustrační úloha |
|
|
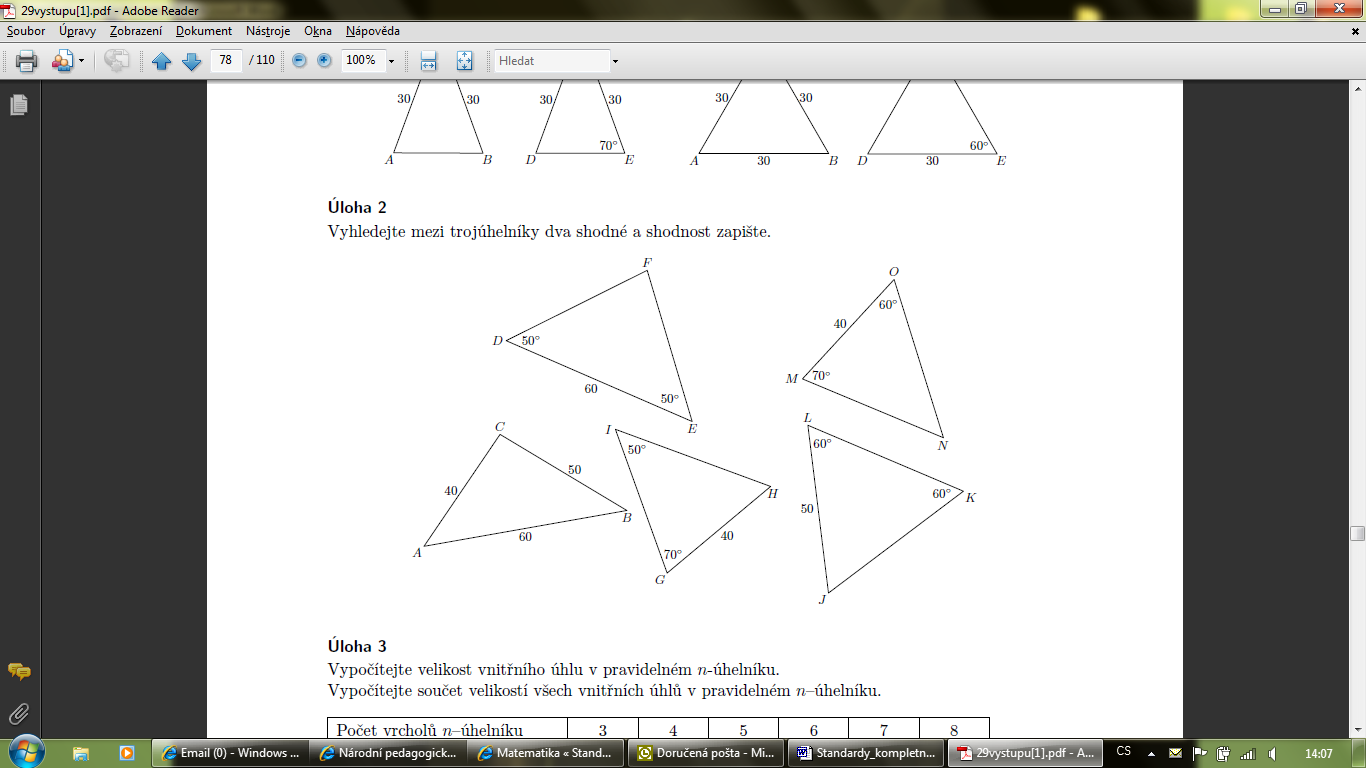
|
|
|
Poznámky |
M-9-3-07.1 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-9-3-08 Žák načrtne a sestrojí obraz rovinného útvaru ve středové a osové souměrnosti, určí osově a středově souměrný útvar |
|
Indikátory |
1.žák rozhodne, zda je útvar osově souměrný 2.žák určí osy souměrnosti rovinného útvaru 3.žák rozhodne, zda je útvar středově souměrný 4.žák určí střed souměrnosti 5.žák načrtne a sestrojí obraz rovinného útvaru ve středové a osové souměrnosti |
|
Ilustrační úloha |
|
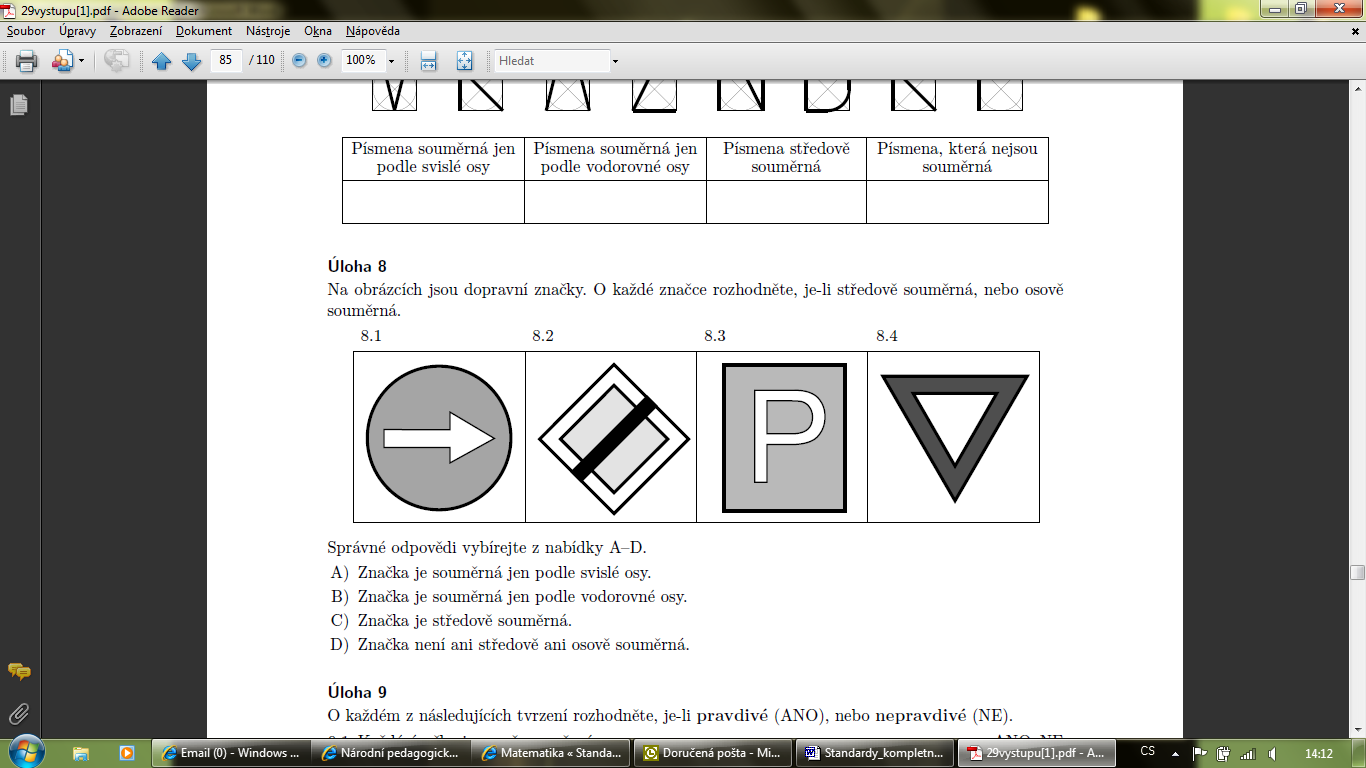
|
|
|
|
Poznámky |
M-9-3-08.1 M-9-3-08.3
Indikátor 5 nelze testovat elektronicky. |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
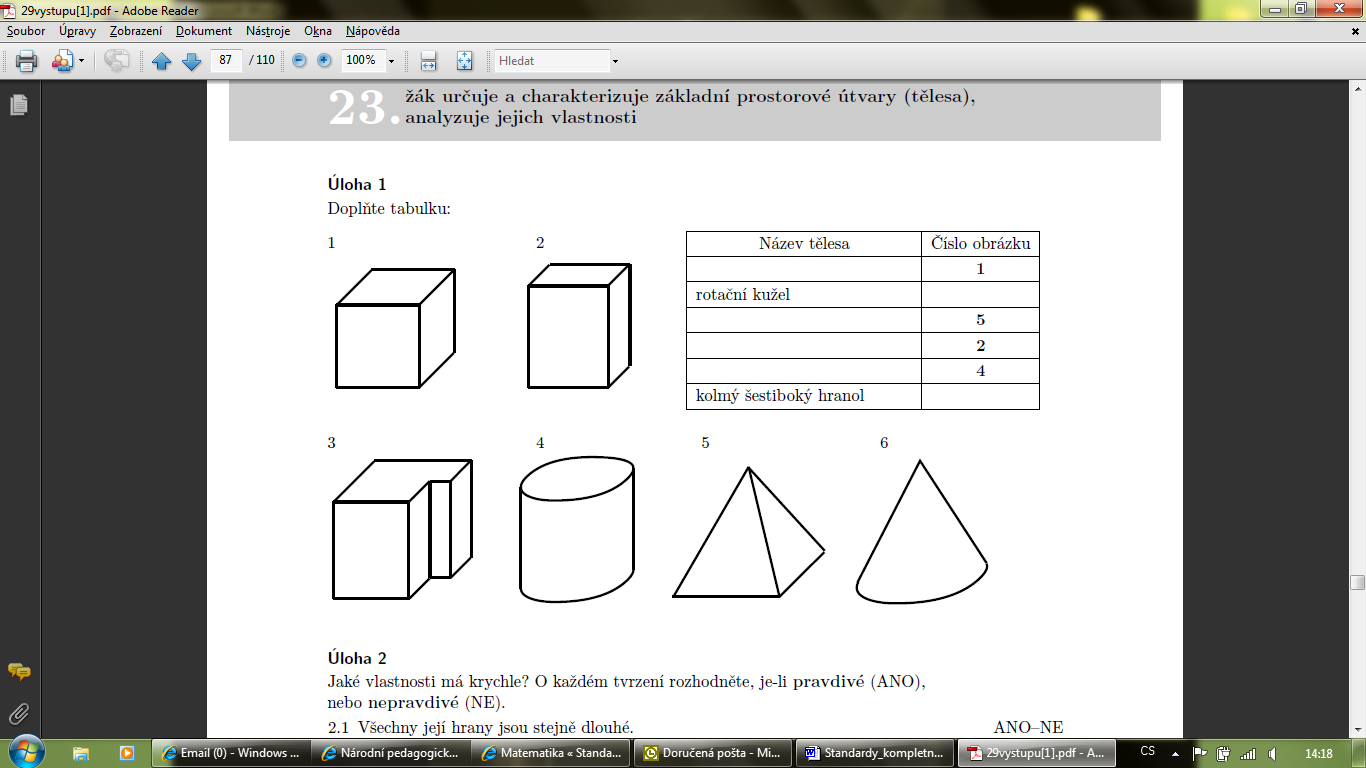
M-9-3-09 Žák určuje a charakterizuje základní prostorové útvary (tělesa), analyzuje jejich vlastnosti |
|
Indikátory |
1.žák rozpozná mnohostěny (krychle, kvádr, kolmý hranol, jehlan) a rotační tělesa (válec, kužel, koule) 2.žák používá pojmy podstava, hrana, stěna, vrchol, tělesová a stěnová úhlopříčka 3.žák využívá při řešení úloh metrické a polohové vlastnosti v mnohostěnech a rotačních tělesech 4.žák pracuje s půdorysem a nárysem mnohostěnů a rotačních těles
|
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-3-09.1 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
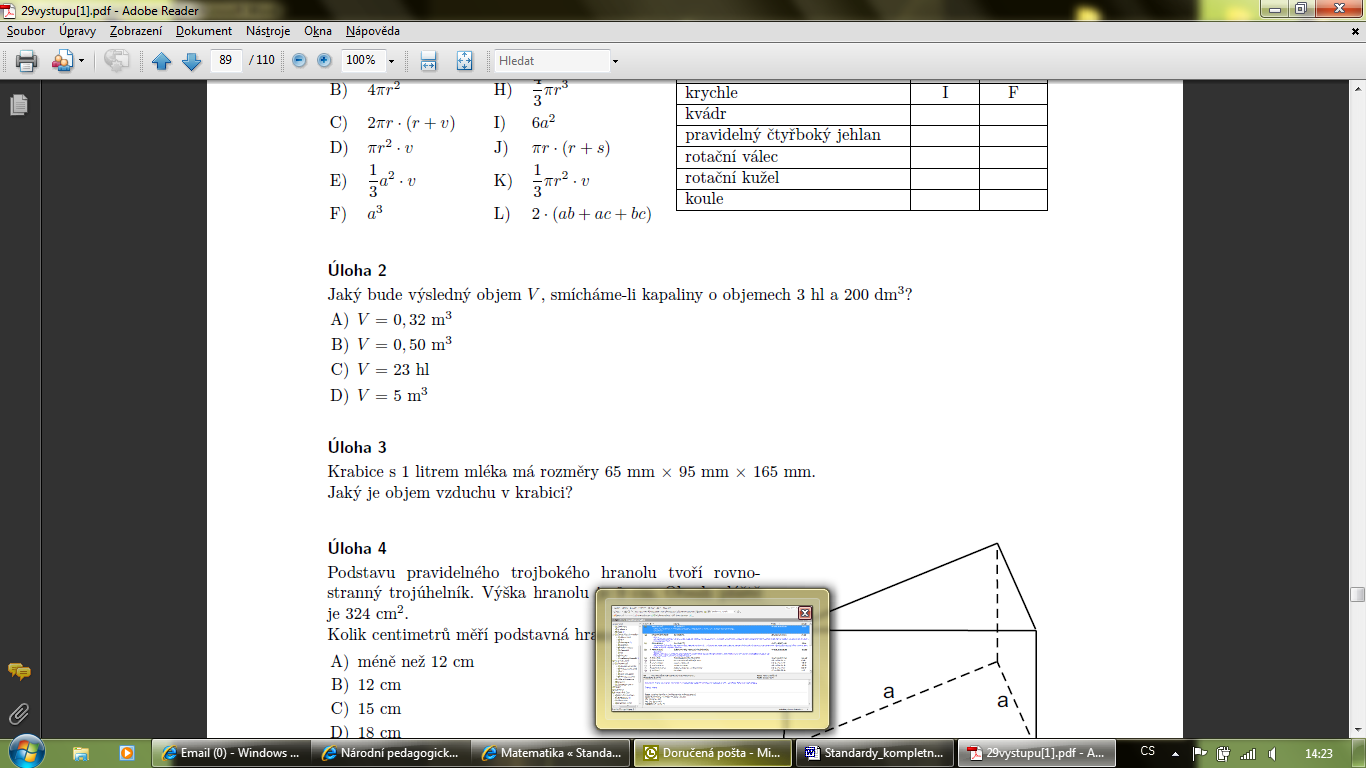
M-9-3-10 Žák odhaduje a vypočítá objem a povrch těles
|
|
Indikátory |
1.žák odhaduje a vypočítá povrch mnohostěnů a rotačních těles 2.žák odhaduje a vypočítá objem mnohostěnů a rotačních těles 3.žák používá a převádí jednotky objemu |
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-3-10.3 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
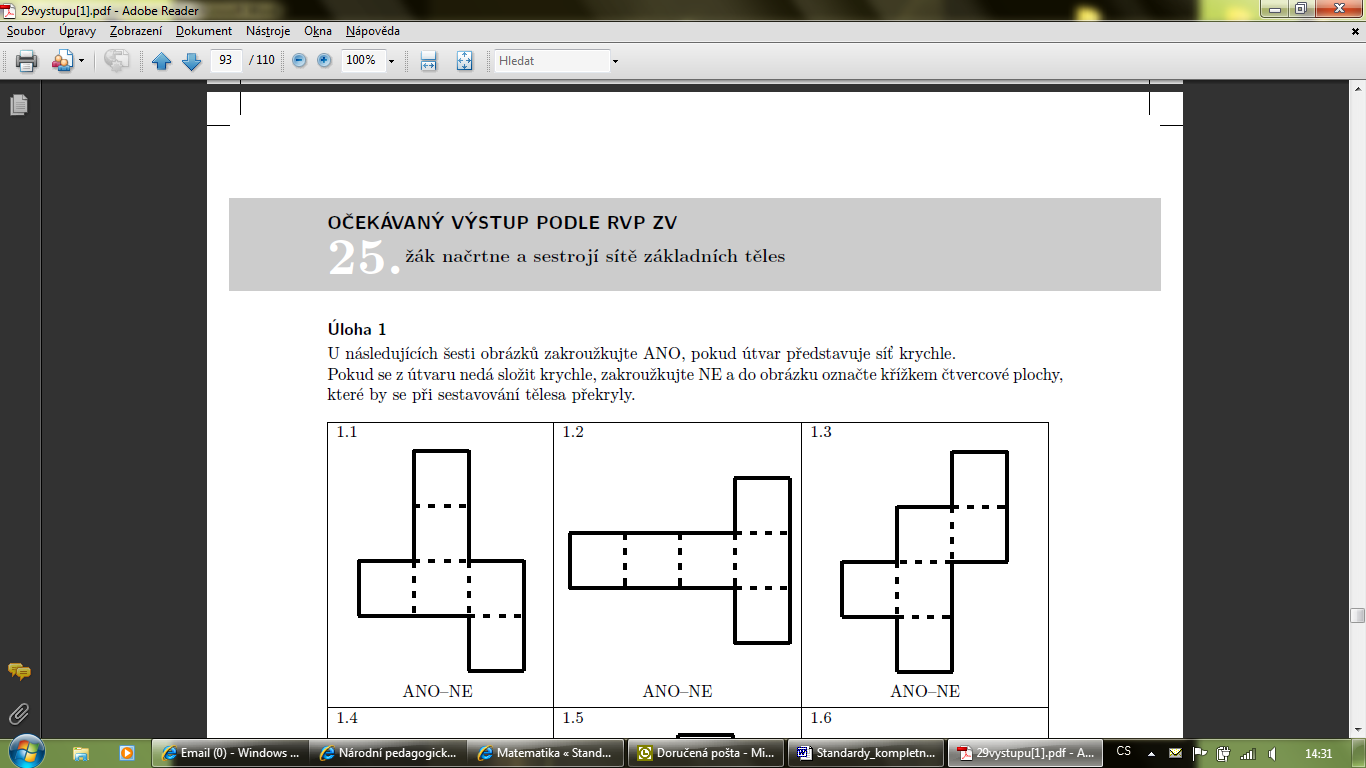
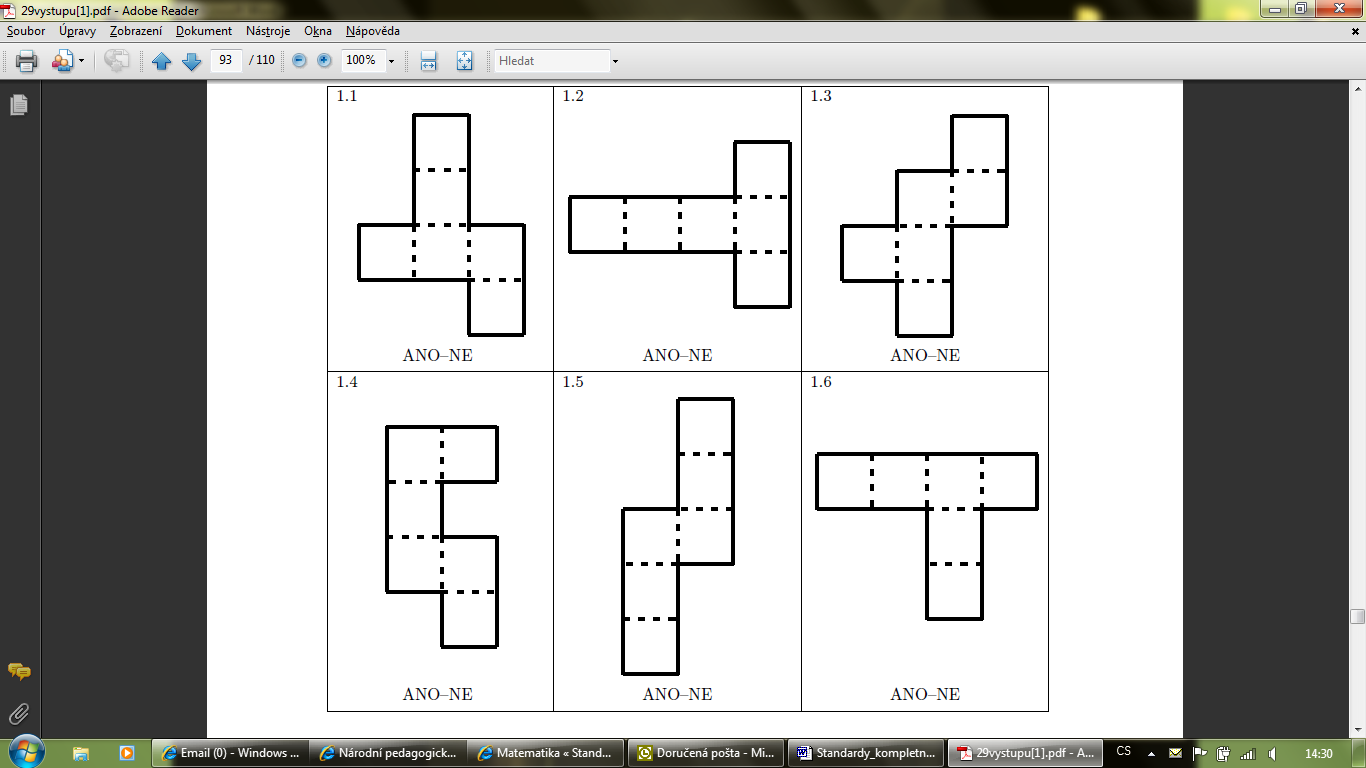
M-9-3-11 Žák načrtne a sestrojí sítě základních těles |
|
Indikátory |
1.žák objasní pojmy síť tělesa, plášť, podstava 2.žák rozpozná sítě základních těles (krychle, kvádr, kolmý hranol, jehlan, válec, kužel) 3.žák načrtne a sestrojí sítě základních těles |
|
Ilustrační úloha |
|
|
|
|
|
Poznámky |
M-9-3-11.2
Indikátor 1 lze testovat pouze otevřenou úlohou.
Indikátor 3 nelze testovat elektronicky. |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-9-3-12 Žák
načrtne a sestrojí
obraz jednoduchých těles v rovině
|
|
Indikátory |
1.Žák rozpozná z jakých základních těles je zobrazené těleso složeno 2.Žák načrtne a sestrojí obraz jednoduchých těles ve volném rovnoběžném promítání
|
|
Ilustrační úloha |
|
|
Popiš, z jakých základních těles je zobrazené těleso složeno.
|
|
|
Poznámky |
M-9-3-12.1
Indikátor 2 nelze testovat elektronicky. |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Geometrie v rovině a prostoru |
|
Očekávaný výstup RVP ZV |
M-9-3-13 Žák analyzuje a řeší aplikační geometrické úlohy s využitím osvojeného matematického aparátu |
|
Indikátory |
1.žák vyhledá v textu úlohy potřebné údaje a vztahy 2.žák volí vhodné matematické postupy pro řešení úlohy 3.žák vyhodnotí výsledek úlohy |
|
Ilustrační úloha |
|
|
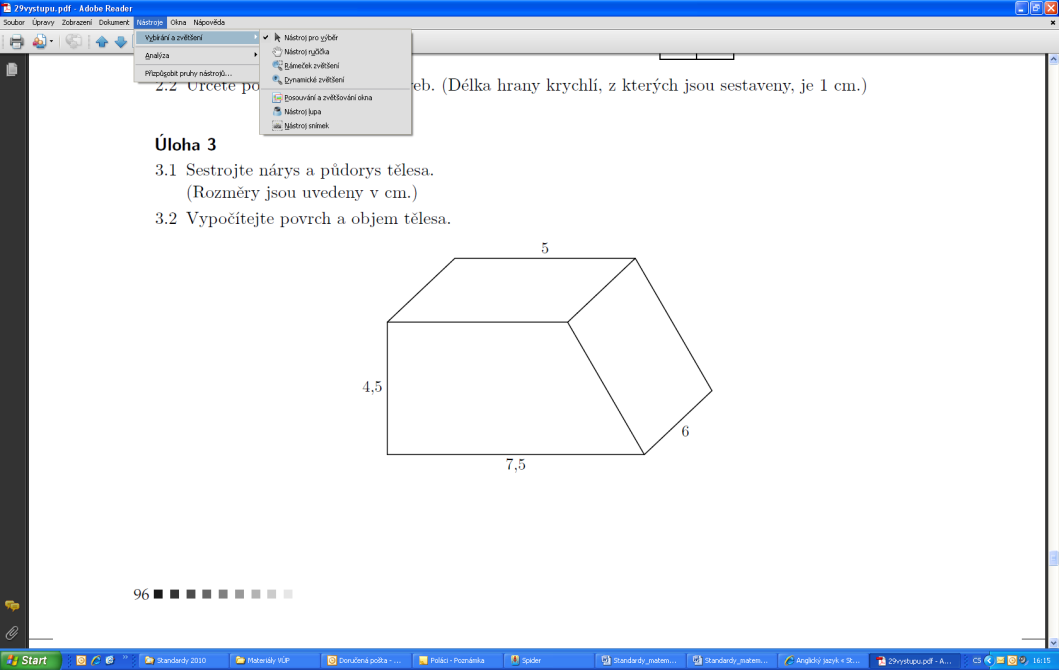
Tenisové míčky o průměru 7 cm se prodávají ve válcových krabičkách po třech. Vypočítejte objem krabičky.
 |
|
|
Poznámky |
M-9-3-13.1 M-9-3-13.2 |
4. NESTANDARDNÍ APLIKAČNÍ ÚLOHY A PROBLÉMY
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Nestandardní aplikační úlohy a problémy
|
|
Očekávaný výstup RVP ZV |
M-9-4-01 Žák užívá logickou úvahu a kombinační úsudek při řešení úloh a problémů a nalézá různá řešení předkládaných nebo zkoumaných situací |
|
Indikátory |
1.žák provede rozbor úlohy a vyhledá v textu úlohy potřebné údaje a vztahy 2.žák zvolí vhodný postup řešení 3.žák provede diskusi o počtu řešení daného problému a kontrolu reálnosti výsledku 4.žák zformuluje odpověď na zadaný problém |
|
Ilustrační úloha |
|
|
Šachového turnaje se zúčastnilo pět hráčů. Kolik bylo sehráno partií, když hrál každý s každým jednou?
|
|
|
Poznámky |
M-9-4-01.1 M-9-4-01.2 M-9-4-01.4 |
|
Vzdělávací obor |
Matematika a její aplikace |
|
Ročník |
9. |
|
Tematický okruh |
Nestandardní aplikační úlohy a problémy
|
|
Očekávaný výstup RVP ZV |
M-9-4-02 Žák řeší úlohy na prostorovou představivost, aplikuje a kombinuje poznatky a dovednosti z různých tematických a vzdělávacích oblastí |
|
Indikátory |
1.žák určí reálnou podobu trojrozměrného útvaru z jeho obrazu v rovině 2.žák popíše základní vlastnosti trojrozměrného útvaru podle jeho obrazu v rovině 3.žák využívá získané poznatky a dovednosti při řešení úloh z běžného života |
|
Ilustrační úloha |
|
|
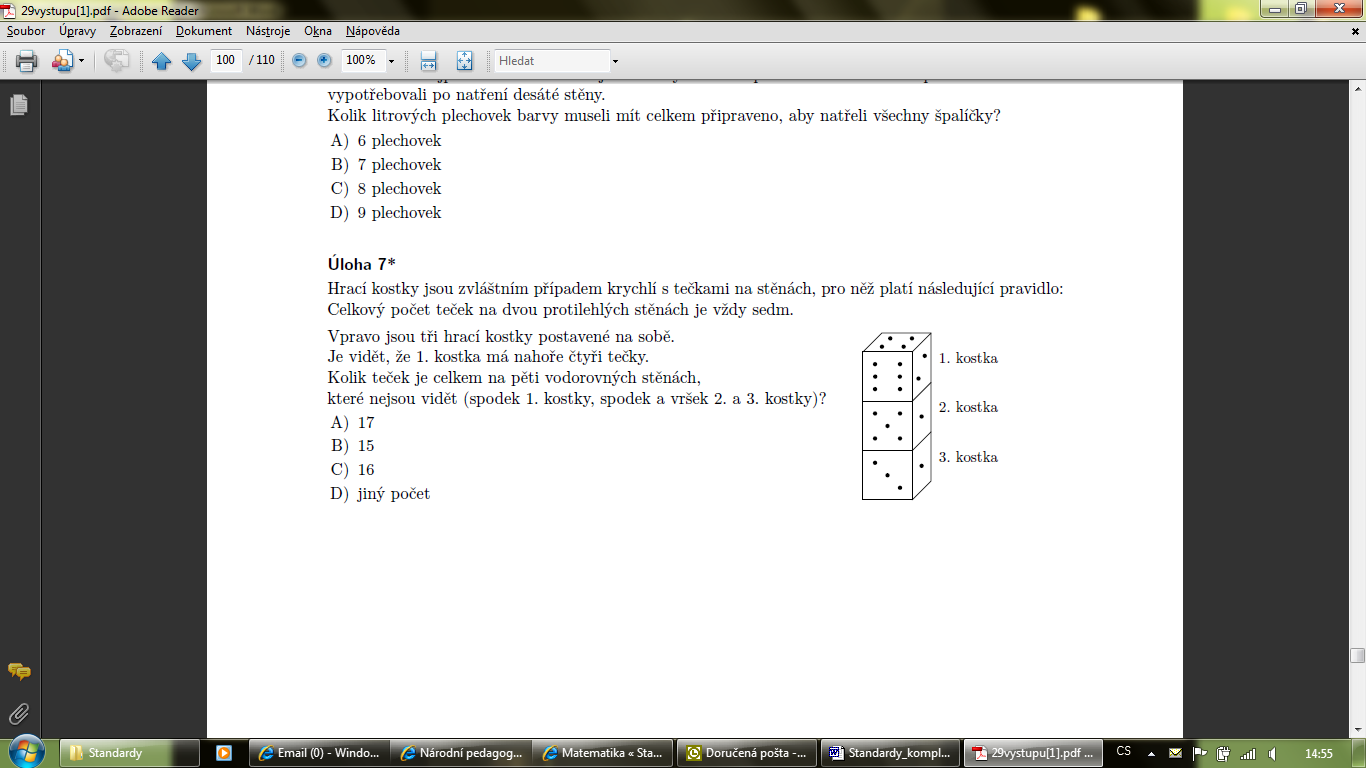
|
|
|
Poznámky |
M-9-4-02.1 M-9-4-02.2 |
"
1 U každého očekávaného výstupu jsou v Poznámkách uvedeny indikátory, které testuje ilustrační úloha. U některých ilustračních úloh jsou pod indikátory uvedeny poznámky pro autory testových úloh. U některých očekávaných výstupů je uvedeno upozornění na to, který indikátor je testovatelný pouze otevřenou úlohou (vyznačeno zelenou barvou) a který testovat elektronicky nelze (vyznačeno červenou barvou).